library(tidyverse)Tutorial 8: Bivariate linear regression
1 Introduction
The ordinary least squares (OLS) or “linear” regression model is probably the workhorse statistical model in (social) data analysis. Countless analyses use it, or variations of it, and all other more advanced models such as logistic regression follow in essence the same logic.
It is therefore important that you know how to estimate and interpret a linear regression model in R, and how you can present the results in your course paper or also a thesis or report. This is what you learn in this tutorial.
Specifically, this tutorial will first walk you through the essential data preparation steps. Then you will see how you estimate a bviariate linear regression model with the lm() function. The last step is to show you how you can present the results in an informative and professional way in your paper.
To illustrate all this, we will study the relationship between how educated people are and how much trust they have in politicians and international institutions using data from the European Social Survey.
Hvis du ønsker å lese en norsk tekst i tillegg: “Lær deg R”, Kapittel 7.
2 Hypotheses
The theory we work with here is that better educated people have more trust in politicians or political institutions, because they have resources (or what sociologists might call “cultural capital”) that allow them to have a deeper understanding of political processes and the underlying processes.1 Also, a higher level of education enables people to deal with situations that are a bit messy or where there are no good options on the table. This should increase an understanding for how politicians and political institutions often work. And this as well should increase trust.
The main alternative hypothesis to be tested is therefore that:
The more years of full-time education someone has completed, the higher their trust in politicians or political institutions.
The corresponding null hypothesis is then:
Education is not related to trust in politicians or political institutions.
3 Setup
3.1 Packages & data download
As always, the first step in an analysis in R is to load all the packages we need (and install those that are not yet installed).
In this tutorial, you will directly work with a full dataset from the European Social Survey (ESS) — not the small practice dataset that you used before. Since the first step will again be to clean and prepare the data, you need the tidyverse package.
To load the package, you just use library() as before:
But you will now also use a new package that you do not yet know: texreg. This is a package that allows you to easily create nice-looking tables that contain the results of your regression models.
To be able to use texreg, you obviously need to install and then load it. Therefore, use install.packages() to install the package — you can run this in your Console since you will do this only once:
install.packages("texreg")When the installation is complete, use library() to load the package and document this in your script file:
library(texreg)3.2 Data import
You should by now know how to import and “trim” ESS data, so this part will be brief and without an example code chunk:
- Use
haven::read_dta()to import the ESS round 7 (2014) dataset; save it asess7in RStudio. - Transform the dataset into the familiar format using
labelled::unlabelled(); - Trim the dataset:
- Keep only observations from Norway;
- Select the following variables:
essround,idno,cntry,trstplt(trust in politicians), andeduyrs; - Use the pipe to link everything;
- Save the trimmed dataset as
ess7;
- If you like, create a data dictionary using
labelled::generate_dictionary();
The two main variables for the main part of this tutorial are trstplt and eduyrs. trstplt measures how much trust people have in politicians in general. Specifically, respondents were asked to rate on a scale from 0 (“No trust at all”) to 10 (“Complete trust”) how much they trust different political institutions and actors — and politicians were one of them. This will be the dependent variable here.
You can learn more about the variable if you use the attributes() function:
attributes(ess7$trstplt)We will use the eduyrs variable to measure people’s level of education. eduyrs measures how many years of full-time education a given respondent has completed. Obviously, this is not a perfectly accurate measurement (some people might spend a lot of time in education, but without success), but it can be used as a proxy (i.e., “approximate measurement”) for education.
Use the data dictionary and the attributes() and other relevant functions to get familiar with the eduyrs variable.
3.3 Data preparation
You might have noticed already that the dependent variable is not stored as a numeric or linear variable but as a factor. This means that you cannot do any calculations with it in this form — and that includes obviously also linear regression.
Therefore, you first have to convert the trstplt variable to a numeric variable. As before, this involves using the as.numeric() function while subtracting 1 to account for the divergence between the text labels and the underlying numerical values:
ess7$trstplt_num <- as.numeric(ess7$trstplt) - 14 Descriptive and bivariate analysis
4.1 Norwegians’ trust in politicians
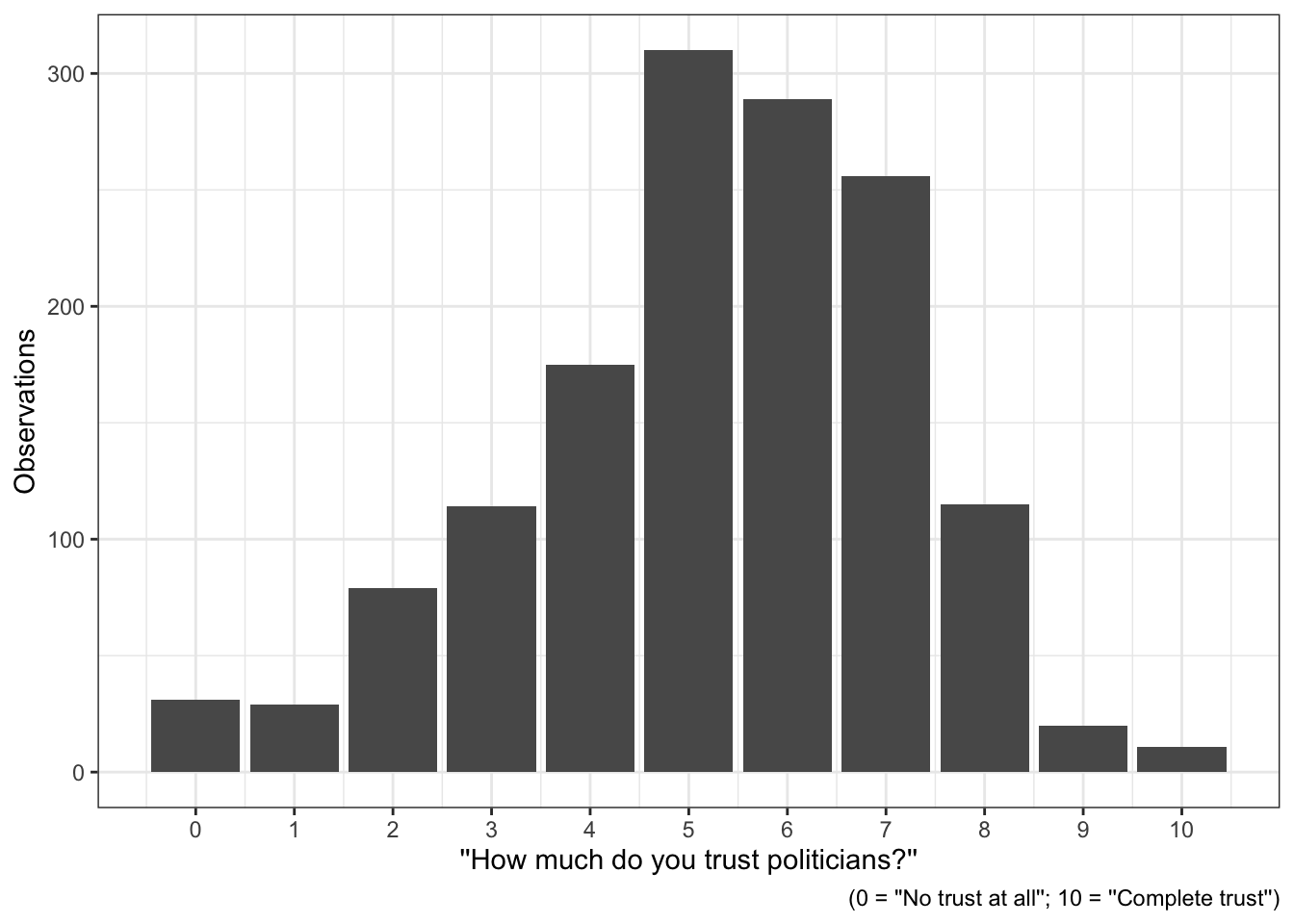
With the new numeric variable in hand, you can create a graph that shows how it is distributed. You should always show this if you are writing a research paper or report:
ess7 %>%
ggplot(aes(x = trstplt_num)) +
geom_bar() +
scale_x_continuous(breaks = seq(from = 0, to = 10, by = 1)) +
labs(x = "''How much do you trust politicians?''",
y = "Observations",
caption = "(0 = ''No trust at all''; 10 = ''Complete trust'')") +
theme_bw()The distribution is concentrated around the mid-to-high values (5-7), which indicates that Norwegians have an overall moderately high level of trust in their politicians. But only very few respondents said they have “complete trust” (10), and there are at least a few respondents that have low levels of trust (0-4).
4.2 Descriptive table
It is also a good idea to give your readers descriptive statistics that help them see how your variables look like. Since you have two numeric or linear variables, a simple table with summary statistics would be appropriate:
bst290::oppsumtabell(dataset = ess7,
variables = c("trstplt_num","eduyrs"))
Variable trstplt_num eduyrs
Observations 1429.00 1434.00
Average 5.26 13.85
25th percentile 4.00 11.00
Median 5.00 14.00
75th percentile 7.00 17.00
Stand. Dev. 1.95 3.72
Minimum 0.00 0.00
Maximum 10.00 30.00
Missing 7.00 2.00You would of course describe this table in more detail in your paper or report, but we will skip this now for the sake of brevity.
4.3 Bivariate analysis
It usually makes sense to do some simpler bivariate tests before you do a (more complicated) regression analysis. Both the dependent and the independent variable are continuous, so the appropriate bivariate test would be to calculate the Pearson correlation coefficient for the two variables and to test if this coefficient is significantly different from 0 (as you know from the previous tutorial):
cor.test(x = ess7$eduyrs,
y = ess7$trstplt_num,
method = "pearson")
Pearson's product-moment correlation
data: ess7$eduyrs and ess7$trstplt_num
t = 5.3783, df = 1425, p-value = 8.779e-08
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.08981487 0.19154010
sample estimates:
cor
0.1410498 The test shows that the two variables are weakly positively correlated with a correlation coefficient of 0.14. Can you tell if this correlation is statistically significant (hint: check the p-value!)?
5 Regression analysis
Now we spent quite a bit of time on the tedious but unfortunately necessary data cleaning part. Luckily, the analysis-part is much more straightforward since R has a built-in function to estimate linear regression models.
The only important thing you need to understand is what a model formula is and how you specify it. This comes now.
5.1 Models & formulas
Whenever you estimate any regression model in R — be it a simple linear regression or more advanced models – you always need to specify the formula for the model.
The formula (or equation) is, in essence, nothing else than a statement about what your dependent and independent variables are and how they are related to each other. In the case here, we expect that people’s trust in politicians (measured via the trstplt_num variable) increases with their level of education (measured with eduyrs).
Expressed as a formula, this would look like this: \[\begin{align*} \texttt{trstplt\_num} = \alpha + \beta_1 \texttt{eduyrs} + \epsilon \end{align*}\]
As you know from the chapters on linear regression in Kellstedt & Whitten (see alternatively Solbakken, Statistikk for Nybeginnere, Chapter 6):
- \(\alpha\) is the intercept (konstantleddet in Norwegian)
- \(\beta_1\) is the regression coefficient (or “slope”, “weight”, regresjonskoeffisient, or stigningstall).
- \(\epsilon\) is the error term — this term captures the variation in the dependent variable that the model cannot explain (see also Solbakken, Statistikk for Nybeginnere, p. 177).
In R, this formula looks much simpler:
trstplt_num ~ eduyrsThere are two interesting things to notice:
We do not use the equal sign (
=) but the tilde (~). This indicates that we do not know if there really is a relationship between the dependent variabletrstplt_numandeduyrs— we are only estimating if there is one!All you have to do is to specify the dependent and the independent variable(s).
Rtakes care of the intercept and the error term automatically.
5.2 Estimating linear regression models: The lm() function
Now that you have the formula for the regression model, you just need to plug it into the R function to estimate linear regression models: the lm() (“linear models”) function.
The lm() function needs as inputs:
- The formula (as just described)
- The dataset that should be used
The following code estimates the model and then saves the result as model1:
model1 <- lm(trstplt_num ~ eduyrs,
data = ess7)R will not automatically show you the results — to see them, you need to print out a summary with summary():
summary(model1)
Call:
lm(formula = trstplt_num ~ eduyrs, data = ess7)
Residuals:
Min 1Q Median 3Q Max
-5.7148 -1.1966 0.0996 1.4332 5.0256
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4.23401 0.19737 21.452 < 2e-16 ***
eduyrs 0.07404 0.01377 5.378 8.78e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 1.932 on 1425 degrees of freedom
(9 observations deleted due to missingness)
Multiple R-squared: 0.0199, Adjusted R-squared: 0.01921
F-statistic: 28.93 on 1 and 1425 DF, p-value: 8.779e-08The output is very R-typical: technical and condensed. Focus on the following:
- The
Coefficients:-table. First, you see two coefficients listed, the(Intercept)andeduyrs. These show you what the model includes: an intercept and a single independent variable (eduyrs). - In the columns to the right, you see
Estimate,Std. Error,t value, andPr(>|t|)printed:- The
Estimates are the coefficients themselves — the \(\alpha\) (for the intercept) and the \(\beta\)s or regression coefficients; - The
Std. Errors are, as the name suggests, the standard errors of the coefficients. - The
t values are the ratios of the coefficients and their standard errors: \(\frac{\texttt{Estimate}}{\texttt{Std. Error}}\).2 You can interpret thet valueslike those from a t-test, only the test here is whether a given coefficient is equal to0or not. Pr(>|t|)are the p-values.- The asterisks are an alternative way to indicate p-values. Three asterisks correspond to a p-value of 0.001 or less. This is also explained in the legend (
Signif. codes)
- The
Kellstedt & Whitten (2018, Chapter 9) or Solbakken (Statistikk for Nybeginnere, Chapters 6 & 8) explain how you make sense of these numbers (also: feel free to ask during class!).
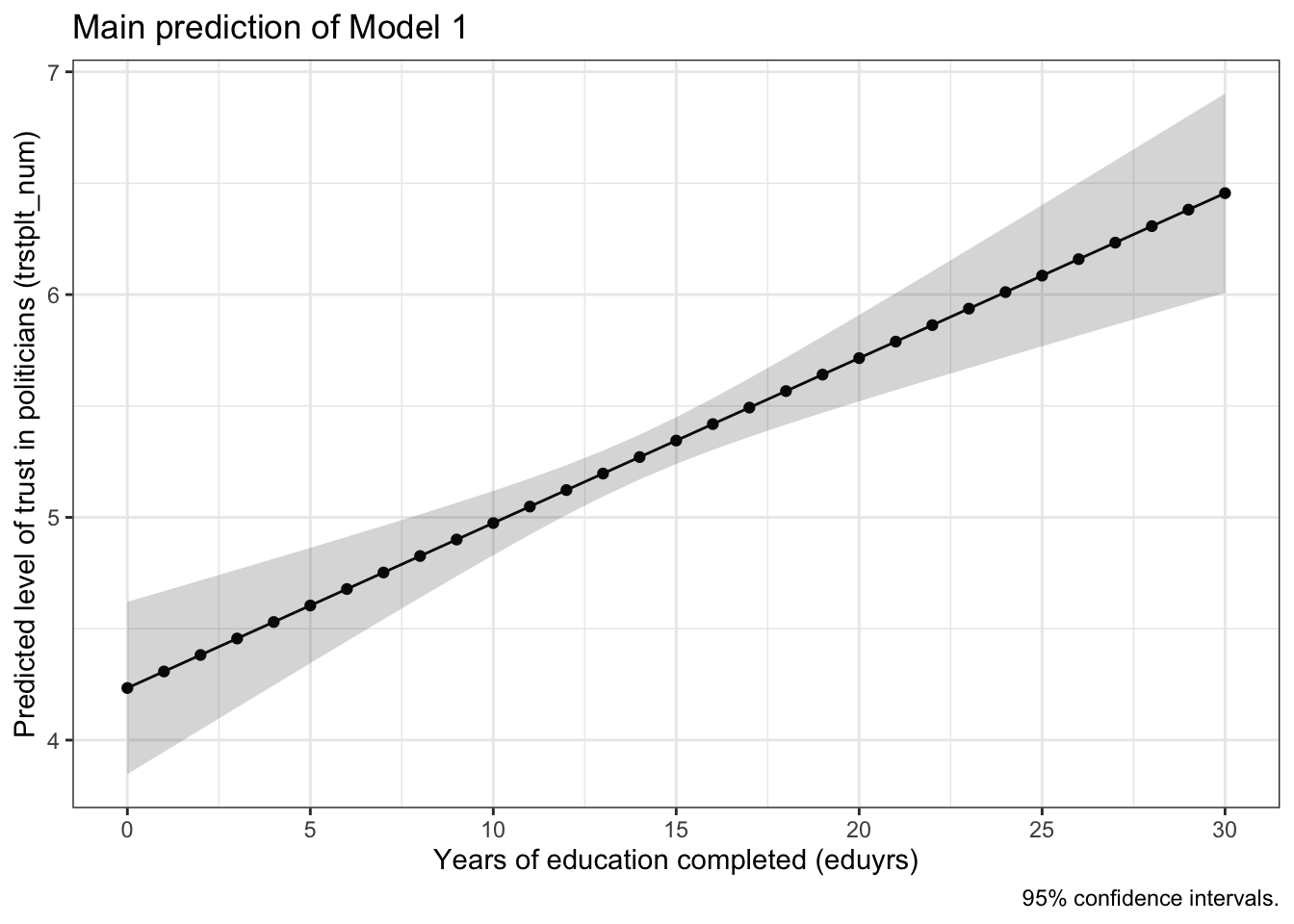
If you find this still difficult to grasp then it might help to look at a visualization of the model’s main result, which is shown in the graph below:
First, focus on the black line with the dots. If you start at the point where eduyrs is zero, you see that the predicted value of trstplt_num is just a bit over 4. If you now go back to the result, is there a similar number?
You can also clearly see that there is a positive relationship between the two variables: As eduyrs increases, trstplt_num increases as well. If you look more carefully, you also see that trstplt_num increases only by a small amount for every additional year of education completed. Can you find out in the detailed results above by how much exactly trstplt_num changes?
You should also notice the gray-shaded area around the black line. This area indicates the confidence intervals for the predicted values. These confidence intervals reflect the fact that we are working with estimates based on a sample. You interpret these the same way as you interpreted the confidence intervall for a sample mean a few weeks ago.
5.3 Presenting the regression results in a publication-quality table
Making sense of the results for yourself is of course only a part of your job as a (social) data analyst. The next step is to present them to the readers of your course paper, thesis, or report.
When you report results like these, you should never simply copy and paste the results from R into your document. Instead, you should always present them in a clean and organized table. And this is in fact quite easy to do with the texreg package that you installed and loaded earlier! This package is specifically designed to transform regression results from R into publication-quality tables.
As a first step, it makes sense to print a preview of the table to your Console. To do this, you use the screenreg() function from the texreg package. Also, the table is supposed to show the results of the model that we estimated earlier (model1), so we specify that within the list (list()) of results we want to have in the table):
screenreg(list(model1))
========================
Model 1
------------------------
(Intercept) 4.23 ***
(0.20)
eduyrs 0.07 ***
(0.01)
------------------------
R^2 0.02
Adj. R^2 0.02
Num. obs. 1427
========================
*** p < 0.001; ** p < 0.01; * p < 0.05The table shows you in essence the same information as the R output above, but in a more organized fashion. You see the coefficient for eduyrs and the intercept plus their standard errors and stars that indicate the corresponding p-values. Further below, you also see summary statistics including the \(R^2\), the adjusted \(R^2\), and the number of observations. At the very bottom, you see a legend that tells you how different stars (asterisks) correspond to different p-values. For example, three asterisks would indicate a p-value of less than 0.001.
You can still make this table a bit prettier by adding proper labels for the coefficients (never report the “raw” coefficient names — your readers don’t know what they mean!)3 and by trimming the significance stars (one is enough):
screenreg(list(model1),
custom.coef.names = c("Intercept",
"Years of educ. completed"),
stars = 0.05)
===================================
Model 1
-----------------------------------
Intercept 4.23 *
(0.20)
Years of educ. completed 0.07 *
(0.01)
-----------------------------------
R^2 0.02
Adj. R^2 0.02
Num. obs. 1427
===================================
* p < 0.05This version is O.K. for now. Next, you use the wordreg() function to export the table to a Microsoft Word document. The settings stay the same, but you now also need to specify a name for the Word document that will contain your table with the file-option:
wordreg(list(model1),
custom.coef.names = c("Intercept",
"Years of educ. completed"),
stars = 0.05,
file = "bivariate_model.doc")And done! If you open that document, you should see the final table with the results (which you can polish more in Word).
6 Conclusion
Now you know how to estimate and interpret a linear regression model in R.
In addition, you also know how to present the results of your regression analysis in a useful and profession way. Don’t underestimate how relevant this is — this is one of these famous “communication” skills that people keep talking about!
As always, you find de-bugging exercises in the usual place. When you do the de-bugging tutorial on bivariate regression, you will look into a different research question: Why are some people happier than others?
Footnotes
See e.g., Bourdieu, P. (1985). The forms of capital. In Richardson, J. G., editor, Handbook of Theory and Research for the Sociology of Education, pages 241–258. Greenwood, New York; Brady, H. E., Verba, S., and Schlozman, K. L. (1995). Beyond SES: A resource model of political participation. American Political Science Review, 89(2):271–294.↩︎
See for yourself: Divide a coefficient by its standard error and see what the result is.↩︎
I’m only doing this here to help you make sense of the code and the results. I would not do this in a research article that I want to publish.↩︎