library(tidyverse) # for data management & visualization
library(prediction) # to calculate predicted probabilities
library(margins) # to calculate marginal effects
library(texreg) # to present regression resultsTutorial 11: Logistic regression for binomial dependent variables
1 Introduction
When working as a (social) data analyst, you will often be interested in outcomes that have two distinct values: Did someone vote in the last election or not? Is someone a union member or not? Does a country go to war or experience a coup d’état in a given year or not? You will, in other words, work with dependent variables that are binary or dichotomous.
In addition, your theory for your outcome or dependent variable will often specify several different potential causes. For example, a person’s decision to vote in an election might depend their age (older people tend to be more likely to vote) but also their education or income. This means that you need to use multivariate regression to really test your theory.
You already know what you would use in this case if you had a linear dependent variable: Ordinary least squares (OLS) regression. But one of the central assumptions underlying the OLS model is that the dependent variable must be linear — and this assumption does not hold if you are interested in electoral participation, union membership, or coups.
Instead, you need to use the logistic regression (a.k.a., “logit”) model. The logistic regression model is specifically designed to analyze the effects of multiple independent variables on a binary outcome or dependent variable. An alternative is the probit regression model, which works slightly differently but will usually give you almost identical results.1
In this tutorial, you will learn how you estimate and interpret a logistic regression model. Topic-wise, we continue with the example from tutorial 6 on tabular analysis: Political participation in the form of voting in a national election.
Before you continue here, make sure that you have read and understood the introduction to the logistic regression model in Kellstedt & Whitten (2018, Chapter 12). Otherwise, you may be able to run the code shown here but you will not understand what any of this really means.
2 Hypotheses
As in Tutorial 6, we will look at how political participation differs by gender, and now also if the relationship is robust to controlling for some other variables (age, education, trade union membership). Just to remind you, the theory and hypotheses from Tutorial 6 were as follows:
The guiding hypothesis for this analysis is: Women have higher rates of political participation than men.
The corresponding null hypothesis is that there is no difference between men and women when it comes to political participation.
Similar to Tutorial 6, we study voting as our form of political participation.
2.1 Setup and data management
As always, the start is to load the necessary packages, which are:
The prediction and margins packages may be new to you (if you did not work through the extra part of Tutorial 9 on multivariate linear regression). These two packages are used to convert the results of regression analyses into more intuitive and useful “quantities of interest”, which is especially important when it comes to logistic regression, as you will see further below.
2.2 Data import and initial data cleaning
This part is exactly as before and you should now already know what to do here (see Tutorials 8 and 9 for details):
- Use
haven::read_dta()to import the ESS round 7 (2014) dataset; save it asess7; - Transform the dataset into the familiar format using
labelled:: unlabelled(); - Trim the dataset:
- Keep only observations from Norway;
- Select the following variables:
essround,idno,cntry,vote,eduyrs,agea,mbtru, andgndr; - Use the pipe to link everything;
- Save the trimmed dataset as
ess7;
- If you like, create a data dictionary using
labelled::generate_dictionary();
2.3 Preparing the dependent variable
2.3.1 Getting rid of extra categories
The previous part took care of most of the data cleaning and preparation, but the dependent variable (vote) needs a bit more work. We go over this in detail because the situation here is one that you may often encounter in practice, so it is good to know how to deal with it.
You will see more clearly what the problem is when you let R print out a frequency table of the variable with table():
table(ess7$vote)
Yes No Not eligible to vote
1127 158 150 It turns out that the vote variable has three categories: “Yes”, “No”, and “Not eligible to vote”. This is a problem because the type of logistic regression model we use here works only for dependent variables that have exactly two categories.2
This means that if we want to use the vote variable, we first have to get rid of one category. In this case, it makes sense to get rid of the “Not eligible” category because the people who are not eligible to vote (e.g., immigrants) have by definition a probability of 0 to vote, which means they are not that interesting to us here.
Therefore, we recode the vote variable by setting all cases that fall into the “Not eligible” category to missing (NA). To do that, we use the na_if() function. This function simply takes a variable (specified under x in the function) and replaces all observations that have a particular value (specified under y) with NA. In this case, we create a new version of vote which is NA if the original version of vote is equal to “Not eligible” and then replace the old with the new version in the dataset:
ess7 %>%
mutate(vote = na_if(x = vote,
y = "Not eligible to vote")) -> ess7Important: You obviously need to save the result with the assignment operator. In this case, we use the “reversed” assignment operator and save the dataset with the new version of the vote variable under the old name (ess7).
If we now again tabulate the vote variable, the “Not eligible” category is empty:
table(ess7$vote)
Yes No Not eligible to vote
1127 158 0 But you will also notice another thing: The “Not eligible” category is now empty, and therefore no longer useful. This means we can get rid of it by using droplevels():
ess7$vote <- droplevels(ess7$vote)Another check reveals that the variable is now probably coded and has exactly two categories:
table(ess7$vote)
Yes No
1127 158 2.3.2 Setting the reference category
A last thing: When you run a logistic regression model, R will take one category of the dependent variable as the ‘baseline’ or ‘reference’ category and then estimate the probability of an observation falling into the other category. For example, if the baseline category of vote is “No”, then R will estimate the probability of falling into the “Yes” category. Importantly, R might also go the other direction and take “Yes” as the reference category. In this case, the model will still be correct — but the interpretation might be weird.
To be sure that R picks the correct reference category, it makes sense to set it explicitly. To do this, you use the relevel() function:
ess7$vote <- relevel(ess7$vote,
ref = "No")With this function, we tell R that it should replace the vote variable with a new version of itself, in which “No” is the reference or baseline category.
3 Descriptive statistics
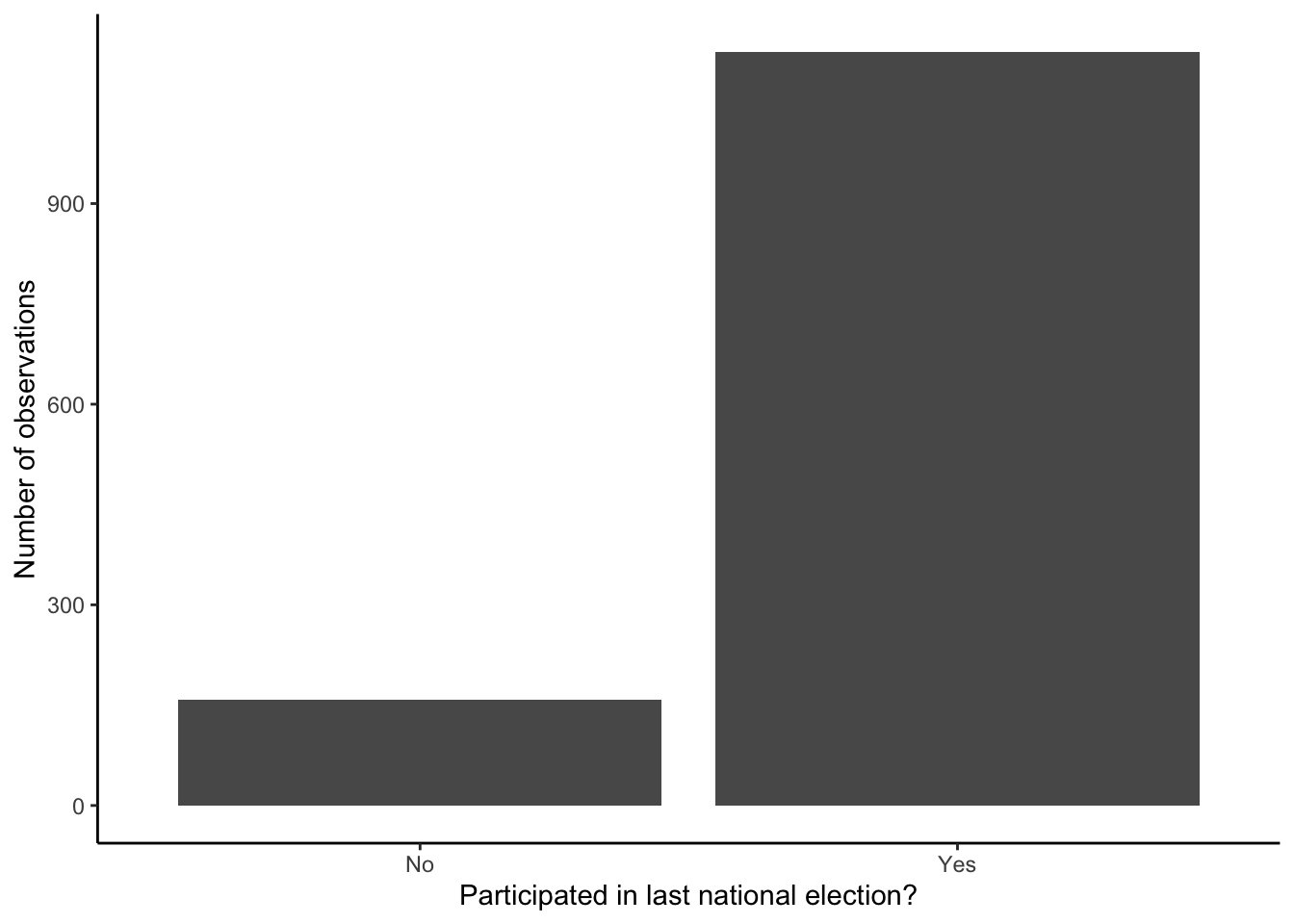
It is always good practice to present your dependent variable to your readers in your report or thesis so that they understand what you are working with. In this case, a bar graph would make sense:
ess7 %>%
drop_na(vote) %>% # we remove the NAs for the graph
ggplot(aes(x = vote)) +
geom_bar() +
labs(x = "Participated in last national election?",
y = "Number of observations") +
theme_classic()Normally, you would now also do more uni- and bivariate analyses using graphs and tables and present these (see e.g., Tutorial 9). For the sake of brevity, however, we will now move straight to the multivariate regression analysis.
4 Multivariate logistic regression
You probably remember that you can run a linear regression in R with the lm() function. Inside this function, you specify the model formula (e.g., income ~ education + age + gender) and the dataset (data = mystudy). Estimating a logistic regression model works almost the same way, with two small but important exceptions.
First, we would not use the lm() function, which is for linear models only. Instead, we use the glm() function, which stands for generalized linear models. The glm() function allows you to estimate regression models where your dependent variable is not linear — for example, logistic regression with a binary variable, but also other types of models for different types of categorical and “non-linear” variables.
And this is also the second difference: We have to tell R what type of dependent variable we have, and what type of model we want to use. We do this by specifying the link function between the dependent variable and the independent variables (see Kellstedt & Whitten 2018, Chapter 12 for a detailed explanation of what a “link function” is) with the family option (“argument”). In our case, because our dependent variable vote is a binomial variable (a categorical variable with two categories) we specify family="binomial".
As in the case of lm(), you first run the model and store the results as a model object. Then you can let R show you a summary of the results with summary().
4.1 Bivariate model
As before, we start with a bivariate model that includes only the main independent variable, gndr:
mod1 <- glm(vote ~ gndr ,
data = ess7, family = "binomial")
summary(mod1)
Call:
glm(formula = vote ~ gndr, family = "binomial", data = ess7)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.8891 0.1144 16.517 <2e-16 ***
gndrFemale 0.1632 0.1709 0.955 0.34
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 958.03 on 1284 degrees of freedom
Residual deviance: 957.12 on 1283 degrees of freedom
(151 observations deleted due to missingness)
AIC: 961.12
Number of Fisher Scoring iterations: 4At first sight, the model results look similar to what you got from lm(): You get coefficient estimates under Estimate, standard errors, p-values, and significance starts in addition to some summary statistics.
But be careful: The coefficient estimates you get from a logistic regression model are logarithmic odds-ratios (or “log-odds”) and these are very difficult to interpret. All you can really directly interpret are the p-values and the signs of the coefficients (are they positive or negative?). In other words, all you can see based on these results is if a variable has a positive or negative effect and if that effect is statistically different from 0 — but the coefficient estimates from a logit model cannot really be interpreted as measures of how strong or weak a given effect is exactly.
In this case, you can see that the dummy for females (which R automatically created) is positively associated with voting (i.e., women have a higher probability of voting than men), but also that the relationship is not statistically significant (and we conclude therefore that there is most likely no difference between men and women).
4.2 Multivariate model
Next, we see what happens when we include the other independent variables and make the model multivariate:
mod2 <- glm(vote ~ gndr + eduyrs + agea + mbtru,
data = ess7, family = "binomial")
summary(mod2)
Call:
glm(formula = vote ~ gndr + eduyrs + agea + mbtru, family = "binomial",
data = ess7)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.923511 0.525497 -1.757 0.0788 .
gndrFemale 0.122934 0.177377 0.693 0.4883
eduyrs 0.114889 0.027353 4.200 2.67e-05 ***
agea 0.034218 0.005432 6.300 2.98e-10 ***
mbtruYes, previously -0.418963 0.245144 -1.709 0.0874 .
mbtruNo -0.553805 0.206417 -2.683 0.0073 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 957.51 on 1282 degrees of freedom
Residual deviance: 880.50 on 1277 degrees of freedom
(153 observations deleted due to missingness)
AIC: 892.5
Number of Fisher Scoring iterations: 5The effect of being a woman is still the same as before: The coefficient is positive, but not significant. Thus, there is probably no difference between men and women when it comes to voting in elections.
But you also see that the other variables have significant effects: Every additional year of education completed significantly raises one’s probability to participate in an election, all else held constant, and so does every additional year of age.
The trade union membership variable is a categorical variable, and thus has a different interpretation: Here the (omitted) baseline or reference category is “Being a union member”, and the displayed coefficients for “Not a member” and “Previously been a member” indicate the differences to that reference category. In this case, having previously been a union member and not being a union member corresponds to a lower chance of participating in an election, and the difference is significant at conventional levels in the case of the “No” category.
4.3 Presenting the results as a table
As in the case of a linear regression analysis before, it is important to present these results in a proper table. And here you can again use the texreg() package:
screenreg(list(mod1,mod2),
stars = 0.05,
custom.coef.names = c("Intercept",
"Female","Years of educ. completed","Age",
"Previous union member","Not a union member"))
==============================================
Model 1 Model 2
----------------------------------------------
Intercept 1.89 * -0.92
(0.11) (0.53)
Female 0.16 0.12
(0.17) (0.18)
Years of educ. completed 0.11 *
(0.03)
Age 0.03 *
(0.01)
Previous union member -0.42
(0.25)
Not a union member -0.55 *
(0.21)
----------------------------------------------
AIC 961.12 892.50
BIC 971.44 923.45
Log Likelihood -478.56 -440.25
Deviance 957.12 880.50
Num. obs. 1285 1283
==============================================
* p < 0.05This is also helpful to you because you get a few more helpful summary statistics like the BIC and AIC information criteria (lower values mean a better-fitting model) and the deviance (a measure that gives you an indication of how far off your model is, comparable to the RMSE in a linear regression model). The log-likelihood is a quite cryptic statistic and primarily used to evaluate the overall significance of your model.3
Still: All you can say is whether a variable has a significant effect, and in which direction that effect goes — but the main problem remains: You cannot say by how large the effect of a variable really is! To do so, you need to calculate predicted probabilities or changes in predicted probabilities — and this comes next.
5 Calculating meaningful quantities of interest
You may remember from the previous tutorials that you can use the prediction and margins packages to calculate predicted values and marginal effects based on a linear regression model result. And you can do the same with a logistic regression model, the only difference is that everything is expressed in predicted probabilities or changes in these probabilities.
5.1 Predicted probabilities
The best place to start is with overall predicted probabilities because these are the most intuitive to interpret. To get these, we use the prediction() function from the prediction package.
When we use this function, we need to specify which model we want to base the prediction on and over which values of which variable. Since our main interest is in the effect of gender, we start by getting the predicted probabilities of voting for men and women based on the multivariate model:
prediction(mod2,
at = list(gndr = c("Male","Female")))Data frame with 2566 predictions from
glm(formula = vote ~ gndr + eduyrs + agea + mbtru, family = "binomial",
data = ess7)
with average predictions: gndr x
Male 0.8711
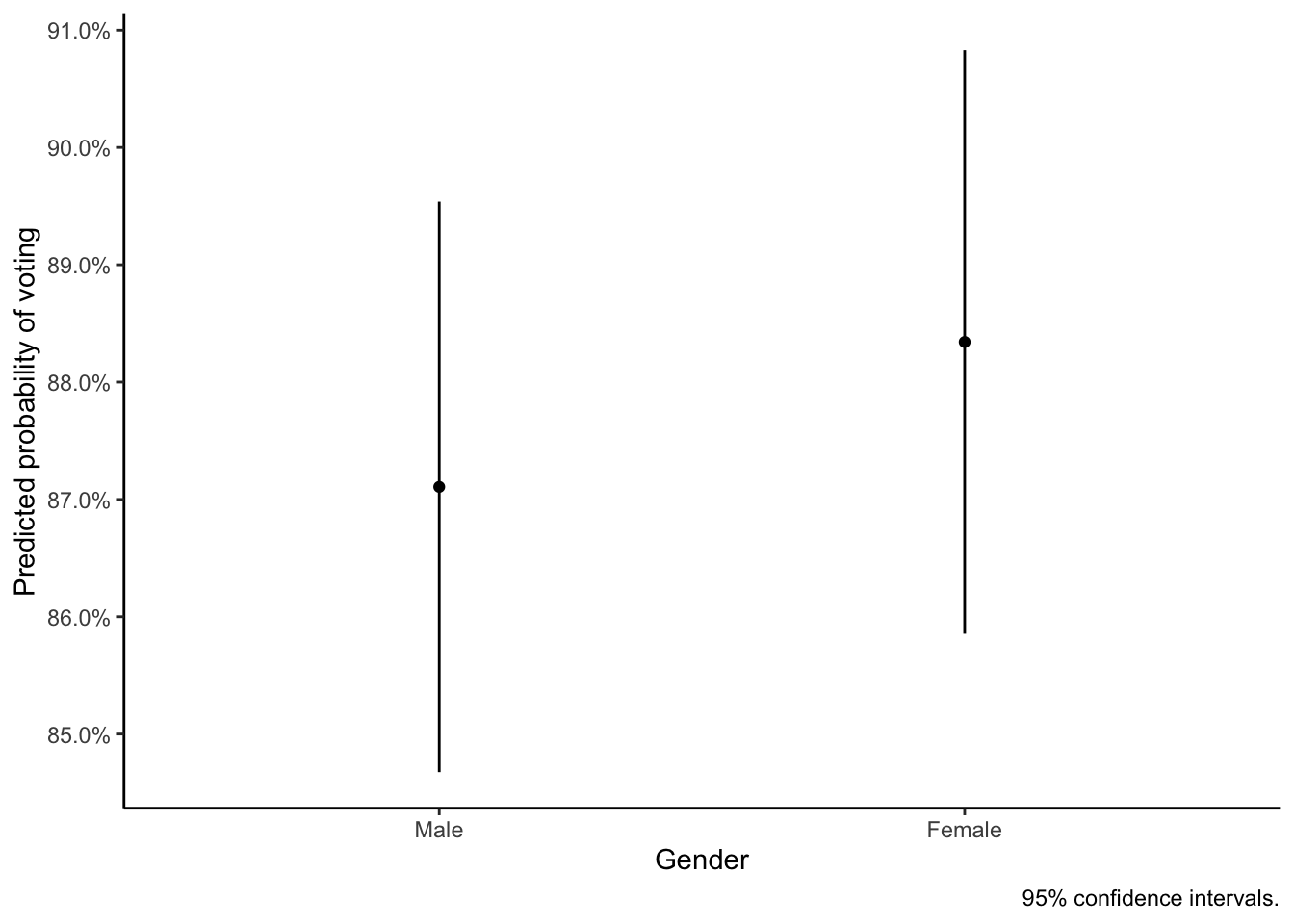
Female 0.8834The numbers you get here are the predicted probabilities of voting in the usual 0-1 notation, where 1 corresponds to 100%. You can see that men have almost exactly the same probability of voting as women: 87% compared to 88%.
To also get measures of uncertainty and statistical significance (p-values & confidence intervals), we can use the prediction_summary() function:
prediction_summary(mod2,
at = list(gndr = c("Male","Female"))) at(gndr) Prediction SE z p lower upper
Male 0.8711 0.01240 70.23 0 0.8468 0.8954
Female 0.8834 0.01269 69.62 0 0.8585 0.9083Here, the p-values tell us that both predicted probabilities are significantly different from 0: We can say that both men and women in the overall Norwegian population have a probability of voting that is higher than 0 (which is arguably not very surprising).
The more interesting (but harder to see) thing is that the confidence interval for one gender include the predicted value of the other gender. For example, the confidence interval for the predicted probability of voting for men includes the predicted value for women. This reflects again the lack of a statistically significant effect of gender.
And this lack of a statistically significant difference between men and women is probably easier to see when you visualize the result (as before, by “piping” the result into a `ggplot() graph):
prediction_summary(mod2,
at = list(gndr = c("Male","Female"))) %>%
ggplot(aes(x = `at(gndr)`, y = Prediction, ymin = lower, ymax = upper)) +
geom_point() +
geom_linerange() +
scale_y_continuous(breaks = seq(.85,.95,.01),
labels = scales::percent) + # to get real percentages
labs(x = "Gender", y = "Predicted probability of voting",
caption = "95% confidence intervals.") +
theme_classic()The conclusion to be drawn here is then obviously that our theory is wrong and we need to stick with the null hypothesis: Gender does not matter for electoral participation.
You can of course use the prediction() function also to get predicted probabilities for numeric independent variables. And, in this case, this also gets us a more interesting result.
For example, let’s look at how the effect of education (eduyrs) on voting when expressed in predicted probabilities. To get these (plus measures of uncertainty), we use the prediction_summary() function and specify a sequence of values of eduyrs over which these should be calculated:
prediction_summary(mod2,
at = list(eduyrs = seq(from = 0, to = 25, by = 1))) at(eduyrs) Prediction SE z p lower upper
0 0.6256 0.078460 7.973 1.547e-15 0.4718 0.7794
1 0.6496 0.071000 9.149 5.764e-20 0.5104 0.7887
2 0.6728 0.063614 10.577 3.811e-26 0.5482 0.7975
3 0.6954 0.056396 12.330 6.234e-35 0.5848 0.8059
4 0.7171 0.049430 14.507 1.099e-47 0.6202 0.8139
5 0.7378 0.042792 17.243 1.266e-66 0.6540 0.8217
6 0.7577 0.036551 20.730 1.857e-95 0.6861 0.8293
7 0.7766 0.030769 25.239 1.514e-140 0.7163 0.8369
8 0.7944 0.025505 31.148 5.406e-213 0.7444 0.8444
9 0.8113 0.020819 38.969 0.000e+00 0.7705 0.8521
10 0.8271 0.016781 49.290 0.000e+00 0.7942 0.8600
11 0.8420 0.013483 62.448 0.000e+00 0.8155 0.8684
12 0.8558 0.011041 77.513 0.000e+00 0.8341 0.8774
13 0.8686 0.009558 90.882 0.000e+00 0.8499 0.8874
14 0.8806 0.009012 97.708 0.000e+00 0.8629 0.8982
15 0.8916 0.009177 97.150 0.000e+00 0.8736 0.9096
16 0.9017 0.009731 92.664 0.000e+00 0.8827 0.9208
17 0.9111 0.010412 87.501 0.000e+00 0.8907 0.9315
18 0.9196 0.011063 83.127 0.000e+00 0.8979 0.9413
19 0.9274 0.011605 79.919 0.000e+00 0.9047 0.9502
20 0.9346 0.012005 77.845 0.000e+00 0.9110 0.9581
21 0.9411 0.012258 76.771 0.000e+00 0.9170 0.9651
22 0.9470 0.012369 76.563 0.000e+00 0.9227 0.9712
23 0.9523 0.012350 77.112 0.000e+00 0.9281 0.9765
24 0.9572 0.012218 78.340 0.000e+00 0.9332 0.9811
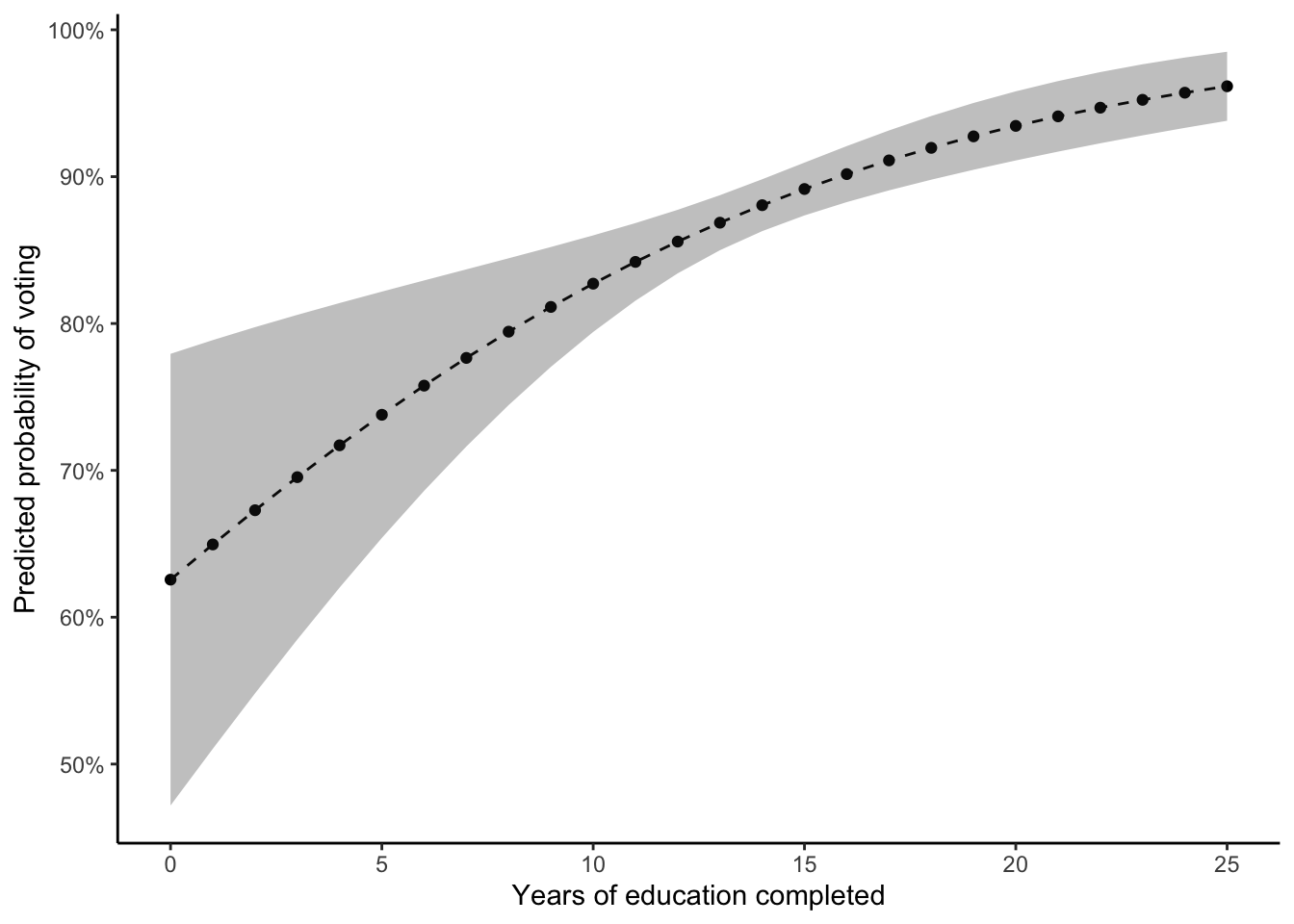
25 0.9616 0.011990 80.194 0.000e+00 0.9381 0.9851If you now look at the numbers under Prediction, you can see how the probability of voting increases from around 62% for someone with no education to around 96% for someone with 25 years of education. That is an increase of more than 30 percentage points, which is not exactly small.
A visualization should again make this even easier to see:
prediction_summary(mod2,
at = list(eduyrs = seq(from = 0, to = 25, by = 1))) %>%
ggplot(aes(x = `at(eduyrs)`, y = Prediction, ymin = lower, ymax = upper)) +
geom_point() +
geom_line(linetype = "dashed") +
geom_ribbon(alpha = .3) +
scale_y_continuous(labels = scales::percent) + # to get real percentages
labs(x = "Years of education completed",
y = "Predicted probability of voting") +
theme_classic()The graph clearly shows the strong increase in the probability to vote as education increases. Also visible is that the estimates are more uncertain (wider confidence intervals) at low values of the eduyrs variable and get narrower for higher values. This most likely reflects that fact that there are only very few observations with less than 10 years of education in the dataset.
5.2 Marginal effects
In addition to the overall predicted probabilities, we would usually also like to know by how much exactly a change in an independent variable changes these probabilities. These marginal effects (i.e., changes in predicted probabilities associated with a change in a given independent variable) are easier to interpret and more similar in nature to the regression coefficients you get from linear regression model.
Getting these marginal effects (plus measures of uncertainty) is possible with the margins_summary() function from the margins package.
You might appreciate the fact that using this function is fairly simple (at least in its basic form):
margins_summary(model = mod2)
factor AME SE z p lower upper
agea 0.0034 0.0005 6.3349 0.0000 0.0024 0.0045
eduyrs 0.0116 0.0028 4.2093 0.0000 0.0062 0.0170
gndrFemale 0.0124 0.0178 0.6951 0.4870 -0.0225 0.0472
mbtruNo -0.0563 0.0216 -2.6089 0.0091 -0.0986 -0.0140
mbtruYes, previously -0.0406 0.0251 -1.6168 0.1059 -0.0897 0.0086All we have to specify here is the model we want to base the calculations on, and the function automatically gives us the changes in the predicted probabilities associated with a given variable.
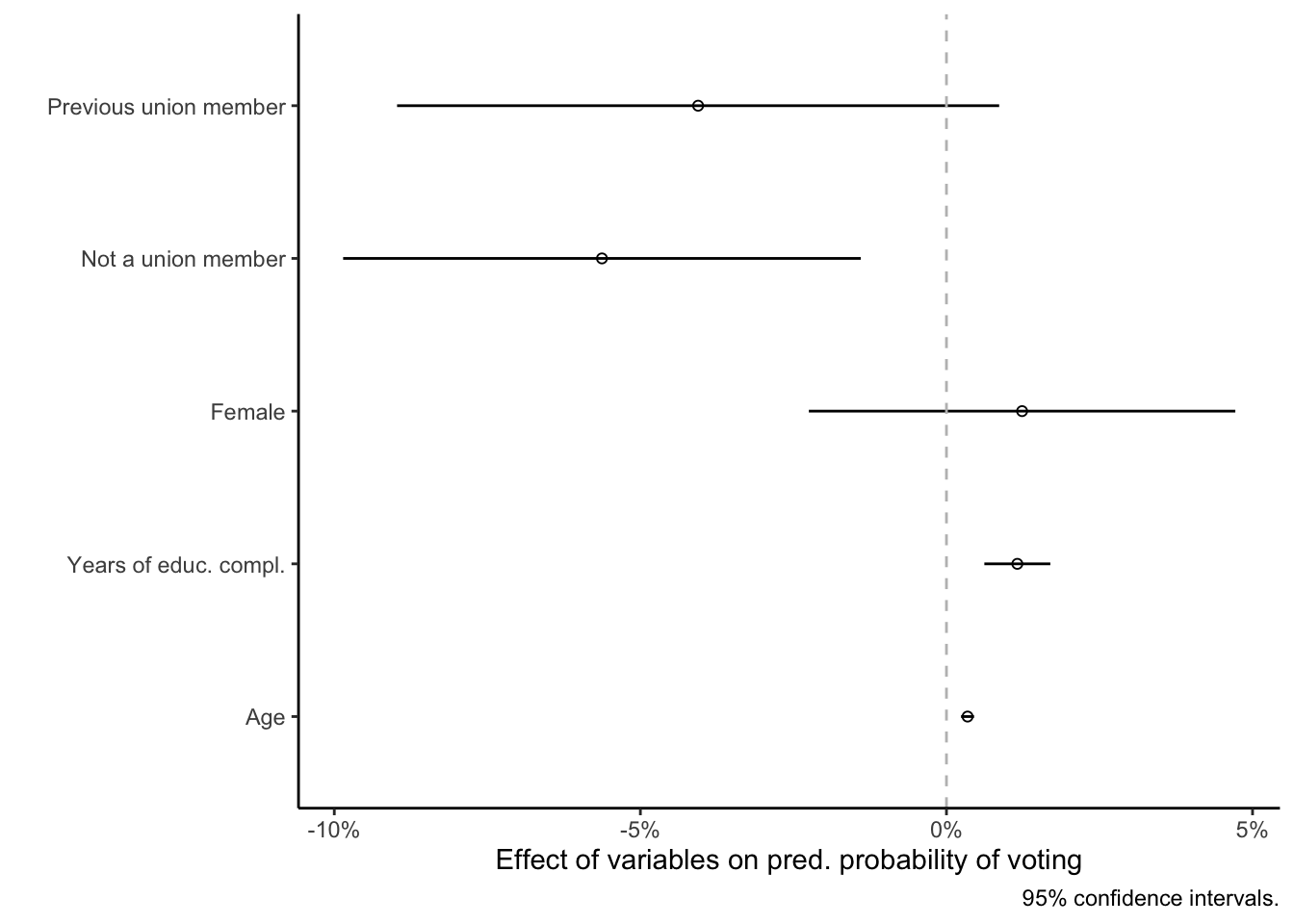
And the result is also fairly easy to interpret: Every additional year of age increases the probability of voting by 0.34 percentage points (0.0034 \(\times\) 100), while every additional year of education increases it by 1.16 percentage points. As the p-values indicate, these effects are significant.
You can also see that the predicted probability of voting for women is about 1.24 percentage points higher than that for men, but again that this is not statistically different from 0. And finally, those who are not a union member or who have previously been members have predicted probabilities of voting that are about 4 and 5.6 percentage points lower compared to current union members.
These results can of course also be visualized:
margins_summary(model = mod2) %>%
ggplot(aes(y = factor, x = AME, xmin = lower, xmax = upper)) +
geom_point(shape = 1) + # shape = 1 gives hollow dots
geom_linerange() +
geom_vline(xintercept = 0, linetype = "dashed", color = "gray") +
scale_y_discrete(labels = c("Age","Years of educ. compl.",
"Female","Not a union member",
"Previous union member")) +
scale_x_continuous(labels = scales::percent) + # to get real percentages
labs(x = "Effect of variables on pred. probability of voting",
y = "", caption = "95% confidence intervals.") +
theme_classic()Again, you see that:
- Gender makes no difference (the effect of being a woman is not significantly different from 0).
- Age and education have positive effects, and these are significantly different from 0.
- Compared to currently being a union member (the omitted baseline category of the union membership variable), having previously been part of a union does not significantly change one’s probability of voting.
- However, not being a union member does significantly reduce the probability of voting compared to the omitted baseline category, being a union member.
Footnotes
If you want a thorough introduction to the logit and probit models as well as a number of other regression models for non-linear dependent variables, you can read Long, J. S. (1997). Regression Models for Categorical and Limited Dependent Variables. Sage, London. To learn about the even more advanced conditional logit model and its extensions, which are often used in research on voter behavior, you can read Train, K. E. (1993). Qualitative Choice Analysis. Theory, Econometrics, and an Application to Automobile Demand. MIT Press, Cambridge, 3rd edition, and Train, K. E. (2009). Discrete Choice Methods with Simulation. Cambridge University Press, Cambridge, 2nd edition.↩︎
There are of course other models for more complex variables, see e.g., Long, J. S. (1997). Regression Models for Categorical and Limited Dependent Variables. Sage, London; or Train, K. E. (1993). Qualitative Choice Analysis. Theory, Econometrics, and an Application to Automobile Demand. MIT Press, Cambridge, 3rd edition.↩︎
You can see if your model as a whole is significantly better at predicting your outcome than random chance or a comparison model by using a likelihood-ratio test (see Long 1997, Chapter 4). To see if your model is better than random chance, you run an “empty” model that includes only an intercept but no explanatory variables (e.g.,
mod0 <- glm(vote ~ 1 , data = ess7)) and then use theanova()function to compare the empty model with your main specification (e.g.,anova(mod0,mod2)). You can use the same procedure to compare two model specifications to each other as long as one is “nested” in the other, meaning that one includes a subset of the variables that are included in the other.↩︎